The war is almost here and people of Winterfell have to decide whom they wish to declare the king in the North. There are one million citizen in Winterfell. These one million citizens need to choose between Daenerys Targaryen and Jon Snow. But there is one man who wish to know the results before hand to maintain his reputation as Master of Whisperers. And he is Lord Varys. Curious to know the outcomes of the decision before hand, Varys sends four thousand crows to random people asking for their opinion as to whom they will choose to be their king. Three thousand of these people choose John Snow while the rest thousand choose Daenerys Targaryen.
Please go through the following post for better understanding of the concept in this post: An Introduction To Machine Learning Introduction to Machine Learning Terminology and Perceptron
Varys has opinion of four thousand people. According to the sample data that he has, the fraction of people voting for Daenerys is 1000/4000 = 0.25. Let’s name this fraction as ν. Being said that, fraction of people voting for Jon is 3000/4000 = 0.75 or 1 – ν.
Okay. We know about the choice of sample set, i.e. four thousand people. But Varys is a man of experience. He ought to know about the inclination of the whole population i.e. one million citizens. Since he can’t ask each citizen his choice, Lord Varys decides to calculate the probability of voting percentage for Daenerys. Let’s call it μ. Then probability of voting percentage for Jon Snow is 1 – μ.
Varys wants to know about μ. But he knows only ν.
So, the question is :
Can ν tell us about μ ?
Before we proceed further, I want you to realise the importance of this question. Because in majority of machine learning problems, we are given with some sample training set and we derive a generic model which applies on whole population. The answer to this question should be Yes. Let’s see how.
The error between these two probabilities can be calculated by |ν – μ|. This error term has to be small in order to answer the question that we ask above as yes. If error is small, we are saying that yes, in sample term can give insight about out of sample term.
How much error term can we tolerate? Or In other words, what is the acceptable value of |ν – μ|?
Varys chooses a tolerance value ε and says that if the error is less than this then his estimation is good and if it’s greater, then his estimation is bad.
|ν - μ| < ε Good Estimation
|ν - μ| > ε Bad Estimation
Varys knows in sample term or ν, but he knows nothing about μ. μ is a probability term. Therefore |ν – μ| is a probability term too. Since Varys doesn’t like to be wrong, he would like the probability of |ν – μ| > ε (or the bad estimation) to be very small. So he refers Hoeffding’s equation to know what is the maximum probability of |ν – μ| > ε.
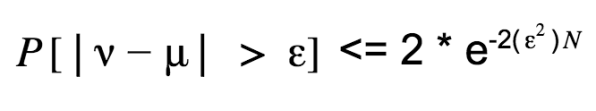
Here N represents the sample value (here it is 4000).
The right hand side of the equation has a negative exponent, so it will reach to a small value quickly. Refer the picture above for the graph of negative exponent. That means, if we have a large N, our negative exponent would reach to a lower value quickly and hence the probability of |ν – μ| > ε would be very less . But if we choose a very small value for ε (which we desire of course), then its square will dampen the effect of N and the right hand side won’t be a very small number. Thus there is a tradeoff between N and ε. We need to choose ε such that it is not too small to lessen the effect of our sample data set count N, and not too big or else it will not be tolerant enough.
Now since Varys needs to be sure about his predictions; he appoints his ten trusted people as sorcerer. Each sorcerer will generate a hypothesis for one million people based on the data of four thousand people. He wants ten different hypothesis or h(x) .
All the sorcerer did their work and they generated 10 different hypothesis, h1(x), h2(x), h3(x), h4(x), h5(x), h6(x), h7(x), h8(x), h9(x), h10(x) for Lord Varys. On our training set, different hypothesis have different accuracy. That is documented below:
| Hypothesis | Number of votes for Daenerys in sample of 4000 | Number of votes for Jon Snow in sample of 4000 | Number of votes for Daenerys by hypothesis of 4000 | Number of votes for Jon Snow by hypothesis of 4000 | Error
in Daenerys votes prediction |
| h1(x) | 1000 | 3000 | 2000 | 2000 | 100% |
| h2(x) | 1000 | 3000 | 1900 | 2100 | 90% |
| h3(x) | 1000 | 3000 | 1800 | 2200 | 80% |
| h4(x) | 1000 | 3000 | 1700 | 2300 | 70% |
| h5(x) | 1000 | 3000 | 1600 | 2400 | 60% |
| h6(x) | 1000 | 3000 | 1500 | 2500 | 50% |
| h7(x) | 1000 | 3000 | 1400 | 2700 | 40% |
| h8(x) | 1000 | 3000 | 1300 | 2700 | 30% |
| h9(x) | 1000 | 3000 | 1200 | 2800 | 20% |
| h10(x) | 1000 | 3000 | 1000 | 3000 | 0% |
So, Is h10(x) the best hypothesis as it is giving 0% error on our given data? How will h10(x) behave on one million data? What’s the deal with other hypothesis? What does Hoeffding has to say about this?
The Hoeffding’s equation won’t apply on many hypothesis. As we have made many hypothesis, there is one hypothesis which gives us 100% success or 0% error. But we still don’t know how our ten hypothesis will act on the real 1 million population. Let’s see modified Hoeffding’s equation in case of multiple hypothesis.
![]()
10 is the number of hypothesis in our case. Let’s generalise the result for M hypothesis(M is 10 in our case)
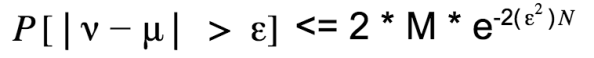
This gives an upper bound on our error probability and as we shall see in generalisation, we should not try hard to fit our result in the given sample set.
Further resource:
Please read earlier part of the series to get a better grasp:
An Introduction To Machine Learning
Introduction to Machine Learning Terminology and Perceptron
https://en.wikipedia.org/wiki/Hoeffding%27s_inequality
If you liked this article and would like one such blog to land in your inbox every week, consider subscribing to our newsletter: https://skillcaptain.substack.com